حل مسئلهٔ 8 وزیر با استفاده از یک الگوریتم ساده + کد پایتون

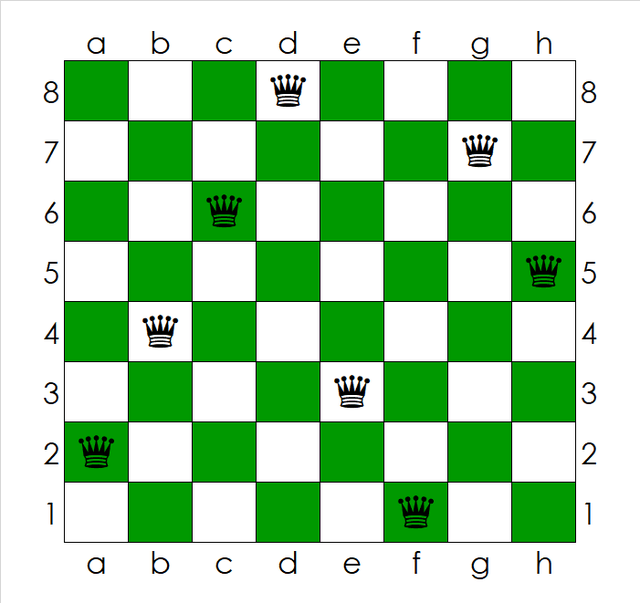
مسئلهٔ ۸ وزیر می‌پرسد که در یک صفحهٔ شطرنج چه‌طور می‌توانیم ۸ مهرهٔ وزیر را چنان قرار دهیم که هیچ‌کدام در معرض تهدید دیگری نباشد. در ریاضیات و علوم کامپیوتر، مسئلهٔ n وزیر یک نسخهٔ تعمیم‌یافته از ۸ وزیر می‌باشد که برای اکثر nهای صحیح مثبت (یا طبیعی) بیش‌تر از یک چینش وجود دارد.

قبلاً یک روش برای پیدا کردن راه حل برای مسئلهٔ ۸ وزیر با استفاده از الگوریتم ژنتیک ارائه دادم. حال می‌خواهم یک روش دیگر برای همین هدف اما به صورت یک الگوریتم قطعی و تصادفی به همراه کد پایتون ارائه دهم.

کد پایتون

from typing import List, Tuple
from pprint import pprint
import random

def empty_slots(board: List[List[int]]) -> List[Tuple[int, int]]:
    result = [(x//8, x%8) for x in range(64)]
    for i, row in enumerate(board):
        for j, slot in enumerate(row):
            if slot != 0:
                for k in range(8):
                    if (j, k) in result:
                        result.remove((j, k))
                    if (k, i) in result:
                        result.remove((k, i))
                for k in range(j, -1, -1):
                    if (k, i-abs(k-j)) in result:
                        result.remove((k, i-abs(k-j)))
                for k in range(j, 8):
                    if (k, i+abs(k-j)) in result:
                        result.remove((k, i+abs(k-j)))
                for k in range(i, -1, -1):
                    if (j+abs(k-i), k) in result:
                        result.remove((j+abs(k-i), k))
                for k in range(i, 8):
                    if (j-abs(k-i), k) in result:
                        result.remove((j-abs(k-i), k))

    return result

if __name__ == "__main__":
    left_queens = 8
    board = None

    while left_queens:
        left_queens = 8
        board = [[0] * 8 for _ in range(8)]

        while True:
            empty = empty_slots(board)
            if len(empty) == 0:
                break
            x, y = random.choice(empty)
            board[y][x] = 1
            left_queens -= 1

    pprint(board)

• تابع empty_slots یک لیست از موقعیت‌هایی را برمی‌گرداند که توسط هیچ وزیری تهدید نمی‌شود.
• صفحهٔ بازی در متغیر board به صورت یک لیست تو‌درتو ذخیره می‌شود. هر عضو لیست داخلی، یک عدد صحیح است که یا یک است (وزیری در آن قرار دارد) یا صفر (خالی است).
• همان‌طور که در کد مشاهده می‌کنید، متغیر left_queens در ابتدا برابر ۸، تعداد کل وزیر‌هایی که باید بدون در معرض تهدید قرار گرفتن در صفحه قرار بگیرند، می‌باشد.
• در حلقهٔ while داخلی ابتدا فهرستی از موقعیت‌هایی که هم خالی هستند (هیچ مهره‌ای در آن وجود ندارد) و هم جزو مکان‌های حملهٔ یک وزیر نیستند توسط تابع empty_slots ساخته می‌شود و در empty ذخیره می‌شود.
• در صورتی که نتوان هیچ وزیر جدیدی را در صفحهٔ بازی قرار داد، حلقهٔ while داخلی شکسته می‌شود.
• یک موقعیت تصادفی از میان موقعیت‌های آزاد با استفاده از random.choice انتخاب می‌شود و در آن یک وزیر قرار داده می‌شود.
• با توجه به این که حلقهٔ while داخلی آخرین جمله (یا دستور) در حلقهٔ while خارجی است؛ کنترل برنامه بلافاصله به اول حلقهٔ while خارجی و بررسی شرطش واگذار می‌شود.
• در شرط حلقهٔ while خارجی تعداد وزیر‌های باقی‌مانده بررسی می‌شود و در صورتی که برابر با صفر نبود، دوباره از اول به جست‌وجوی یک راه حل می‌رود.
• در صورتی که تعداد وزیر‌های باقی مانده برابر صفر باشد، یعنی متغیر ارزش بولی متغیر left_queens برابر نادرست باشد، حلقه while بیرونی نیز شکسته می‌شود و نهایتاً راه حل پیدا شده به خروجی فرستاده می‌شود.

طرز‌ کار تابع empty_slots

• این تابع ابتدا در اولین خطّ خود یک فهرست از تمام موقعیت‌های صفحهٔ شطرنج می‌سازد.
• سپس با بررسی تک‌تک خانه‌های صفحه، آن‌هایی که یک وزیر در خود دارند؛ تمام موقعیت‌هایی که زیر تهدید وزیر است و همچین خود خانهٔ وزیر از فهرست موقعیت‌های خالی حذف می‌شود.

بهینه‌سازی

به طرق مختلف می‌توان کد نوشته شده توسط بنده را بهبود داد و بهینه کرد. بزرگ‌ترین بهینه‌سازی‌ای که به ذهن خودم می‌رسد، این است که تابع empty_slots یک ورودی جدید بپذیرد: موقعیت‌هایی که تا الآن خالی بودند. به این ترتیب می‌توانیم تنها برای دفعهٔ اول، فهرست تمام موقعیت‌ها را به این تابع بدهیم و دفعات بعد، فهرست ساخته شده توسط دور قبلِ حلقه را به تابع بدهیم.