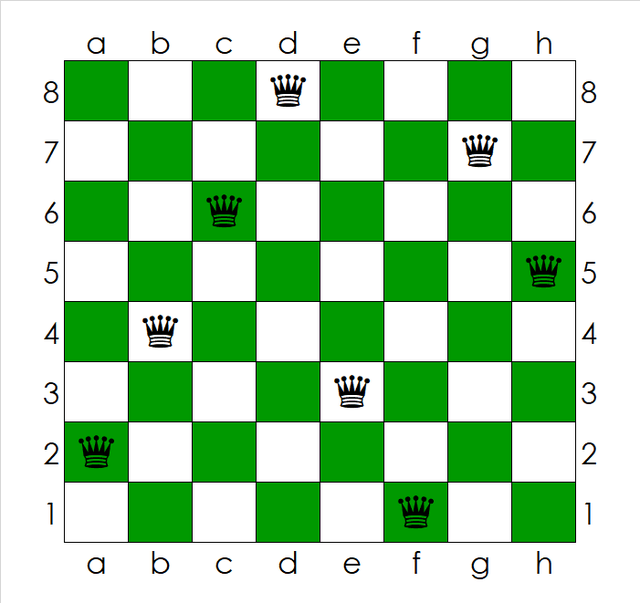
مسئلهٔ ۸ وزیر میپرسد که در یک صفحهٔ شطرنج چهطور میتوانیم ۸ مهرهٔ وزیر را چنان قرار دهیم که هیچکدام در معرض تهدید دیگری نباشد. در ریاضیات و علوم کامپیوتر، مسئلهٔ n وزیر یک نسخهٔ تعمیمیافته از ۸ وزیر میباشد که برای اکثر nهای صحیح مثبت (یا طبیعی) بیشتر از یک چینش وجود دارد.
قبلاً یک روش برای پیدا کردن راه حل برای مسئلهٔ ۸ وزیر با استفاده از الگوریتم ژنتیک ارائه دادم. حال میخواهم یک روش دیگر برای همین هدف اما به صورت یک الگوریتم قطعی و تصادفی به همراه کد پایتون ارائه دهم.
مسئلهٔ ۸ وزیر یک تمرین معروف در علوم کامپیوتر و ریاضیات میباشد. این مسئله در مورد یک صفحهٔ شطرنج رایج و مهرهٔ وزیر در این بازی فکری میباشد. در ریاضیات ثابت میشود که میتوان ۸ وزیر را در یک صفحهٔ شطرنج چنان قرار داد که هیچکدام از وزیرها، دیگری را تهدید نکنند. با تعمیم این مسئله در ریاضیات، ثابت میشود که در یک صفحهٔ شطرنج به ضلع n، میتوان تعداد n وزیر قرار داد؛ چنانچه هیچکدام دیگری را تهدید نکنند. در علوم کامپیوتر میتوان با روشهای مختلفی این مسئله را حل کرد و به یک چینش از مهرههای وزیر رسید که هیچکدام دیگری را تهدید نکنند. یکی از این روشها «الگوریتم ژنتیک» است.