زبانها معمولاً یا تعیین نوع پویا دارند؛ مانند کامن لیسپ، پایتون، جاوا اسکریپت یا دارای تعیین نوع ایستا هستند؛ مانند سی و سیپلاسپلاس، راست و دوباره کامن لیسپ (معمولاً پیادهسازیهای مدرن کامن لیسپ، مانند SBCL، اجازه میدهند بنا به خواست برنامهنویس، قسمتی از کد، دارای تعیین نوع ایستا و قسمتی دارای تعیین نوع پویا باشد).
در پایتون، تعیین نوع متغیرها، مقدار یا مقادیر بازگشتی توابع و متدها و آرگومانهای توابع اجباری نیست. اما میتوانیم با تعیین نوع و استفاده از یک نرمافزار Linter به کاهش خطاهای خود پیش از اجرا کمک کنیم.
def f(x: int) - > int:
return x * 2 + 1با این که تعیین نوع آرگومان یا ورودی تابع f که x باشد و مقدار بازگشت آن یعنی x*2 + 1 در اجرا تأثیری ندارد، اما زمانی که بخواهم مقدار بازگشت تابع f را با یک رشته نویسه (کاراکتر) جمع کنم به من اخطار داده میشود:
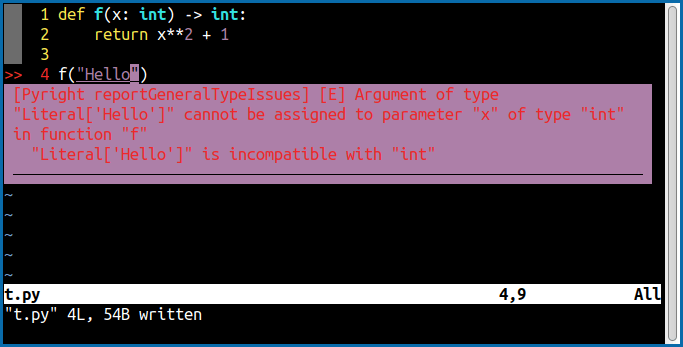
بدیهی است که اجرای این برنامه به وسیلهٔ پایتون نیز باعث خطا میشود. در مقابل زمانی که نوع ورودی و خروجی تابع را مشخص نمیکنم اخطاری داده نمیشود:
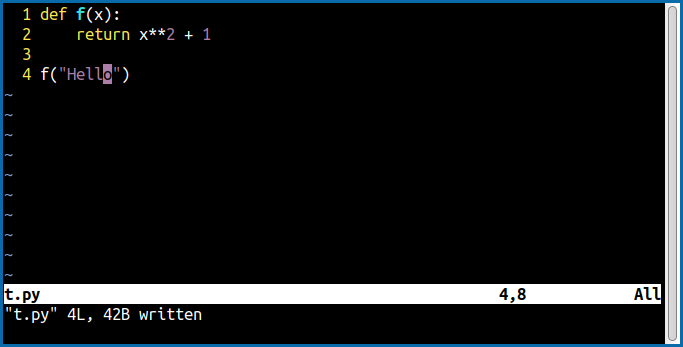
در ادامه با تعیین نوع ورودیها و خروجی توابع و متدها و ویژگیهای یک کلاس آشنا میشویم.
مسئلهٔ ۸ وزیر میپرسد که در یک صفحهٔ شطرنج چهطور میتوانیم ۸ مهرهٔ وزیر را چنان قرار دهیم که هیچکدام در معرض تهدید دیگری نباشد. در ریاضیات و علوم کامپیوتر، مسئلهٔ n وزیر یک نسخهٔ تعمیمیافته از ۸ وزیر میباشد که برای اکثر nهای صحیح مثبت (یا طبیعی) بیشتر از یک چینش وجود دارد.
قبلاً یک روش برای پیدا کردن راه حل برای مسئلهٔ ۸ وزیر با استفاده از الگوریتم ژنتیک ارائه دادم. حال میخواهم یک روش دیگر برای همین هدف اما به صورت یک الگوریتم قطعی و تصادفی به همراه کد پایتون ارائه دهم.
زمانی که از یک برنامهنویس پایتونی بخواهید یک تابع ساده بنویسد تا ارقام یک عدد را جمع کند و برگرداند، احتمالاً ابتدا عدد را به یک رشته تبدیل میکند و سپس رشته را به لیست (فهرست) و نهایتاً تکتک اعضای لیست را که ارقام عدد به صورت رشتههای تکنویسهای هستند به عدد تبدیل میکند و سپس آنها را با هم جمع میکند. ولی الزاماً اولین روشی که برای حل مسئله به ذهنمان میرسد، بهترین روش نیست. در این مطلب دو الگوریتم برای جمع ارقام یک عدد صحیح به صورت بازگشتی و تکرارشونده به همراه کد های پایتون آن ها ارائه میدهم.
