مسئلهٔ ۸ وزیر یک تمرین معروف در علوم کامپیوتر و ریاضیات میباشد. این مسئله در مورد یک صفحهٔ شطرنج رایج و مهرهٔ وزیر در این بازی فکری میباشد. در ریاضیات ثابت میشود که میتوان ۸ وزیر را در یک صفحهٔ شطرنج چنان قرار داد که هیچکدام از وزیرها، دیگری را تهدید نکنند. با تعمیم این مسئله در ریاضیات، ثابت میشود که در یک صفحهٔ شطرنج به ضلع n، میتوان تعداد n وزیر قرار داد؛ چنانچه هیچکدام دیگری را تهدید نکنند. در علوم کامپیوتر میتوان با روشهای مختلفی این مسئله را حل کرد و به یک چینش از مهرههای وزیر رسید که هیچکدام دیگری را تهدید نکنند. یکی از این روشها «الگوریتم ژنتیک» است.
کد به زبان پایتون
# Code by Farooq Karimi Zadeh under MIT/X11
import random
from typing import List, Tuple
Fitness = float
class Chromosome:
possible_rows = tuple(2**i for i in range(8))
def __init__(self, r: str):
if len(r) != 64:
raise ValueError("r must be a string of length 64 exactly")
if r.replace("0", "").replace("1", "") != "":
raise ValueError("r must be a binary string having only 1 or 0")
self._board: List[int] = list()
while len(r):
self._board.append(int(r[:8], 2))
r = r[8:]
def fitness(self) -> Fitness:
max_collisions: int = 64
collisions: int = 0
for i, row_a in enumerate(self._board):
for j, row_b in enumerate(self._board):
if row_a == row_b and i != j:
collisions += 1
for i, row_a in enumerate(self._board):
for j, row_b in enumerate(self._board):
if i == j:
continue
row_p1 = row_a << abs(i-j)
row_p2 = row_a >> abs(i-j)
if row_b == row_p1:
collisions += 1
if row_b == row_p2:
collisions += 1
return (max_collisions - collisions) / max_collisions
def __add__(self, other):
r0 = repr(self)
r1 = repr(other)
def cut(r: str, i: int) -> Tuple[str, str]:
return r[:i], r[i:]
cross_point: int = random.randrange(8, len(r0) - 1, 8)
r0_left, r0_right = cut(r0, cross_point)
r1_left, r1_right = cut(r1, cross_point)
C = Chromosome
return C(r0_left + r1_right), C(r1_left + r0_right)
def __repr__(self) -> str:
return "".join(bin(r).replace("0b", "").zfill(8) for r in self._board)
def mutate(self):
i = random.choice(self.possible_rows)
j = random.randint(0, len(self._board) - 1)
self._board[j] = i
@staticmethod
def rand():
ch = Chromosome("0"*64)
ch._board = list()
for _ in range(8):
ch._board.append(random.choice(Chromosome.possible_rows))
return ch
class GA8:
def __init__(self, pop_size: int, max_gen: int, mutation_rate: float):
self._population: List[Chromosome] = []
self.max_gen: int = max_gen
self.mutation_rate: float = mutation_rate
for _ in range(pop_size):
self._population.append(Chromosome.rand())
def run(self):
for generation in range(self.max_gen):
print("Gen:", generation)
evaled: List[Tuple[Chromosome, Fitness]] = [(C, C.fitness()) for C in self._population]
offsprings: List[Tuple[Chromosome, Fitness]] = list()
for index, ch_ft in enumerate(evaled[:-1]):
next_ch, _ = evaled[index+1]
ch = ch_ft[0]
of0, of1 = ch + next_ch
of0_ft = of0.fitness()
of1_ft = of1.fitness()
offsprings.append((of0, of0_ft))
offsprings.append((of1, of1_ft))
total: list = evaled + offsprings
total.sort(key=lambda e: e[1], reverse=True)
total = total[:len(self._population)]
total = [ch[0] for ch in total]
self._population = total[:len(self._population)]
for ch in self._population:
if random.random() <= self.mutation_rate:
ch.mutate()
if self._population[0].fitness() == 1.0:
break
print("Best ft:", self._population[0].fitness())
def best(self):
return max(self._population, key=lambda ch: ch.fitness())سعی شده کد تا جای ممکن بهینه و استاندارد نوشته شود. همانطور که مشاهده میکنید در کلاس Chromosome طرز ذخیرهٔ یک راه حل مسئله، فهرستی ۸ تایی از اعداد صحیح است. هر عدد صحیح نشاندهندهٔ یک ردیف در صفحهٔ شطرنج است و میتواند از ۰ تا حداکثر ۲۵۵ باشد که حداکثر مقدار برای یک عدد صحیح ۸ بیتی است. همانطور که احتمالاً حدس زدهاید، بیتهایی که ۱ هستند این معنی را میدهند که در موقعیت مورد نظر وزیری وجود دارد و یک بیت ۰ به این معنی است که هیچ مهرهای در آن خانه وجود ندارد.
کلاس Chromosome
متد __init__ کلاس کروموزوم (فامتن) فکر نمیکنم نیازی به توضیح داشته باشد. متد rand یک متد استاتیک (ایستا) است و یک کروموزوم تصادفی میسازد. همانطور که احتمالاً متوجه شدید، کروموزومی که به صورت تصادفی ساخته میشود، به هیچ وجه در آن دو وزیر در یک ردیف قرار نمیگیرند (هر عدد صحیح، یکی از توانهای دو است. در نتیجه در شکل دودویی، هر کدام از آنها تنها یک بیت برابر ۱ است). این خود به حل سریعتر مسئله کمک میکند چرا که فضای جستجو(search space) را تقلیل دادیم.
متد __add__ هم همانطور که مشخص است کار ازدواج(یا جفتگیری) دو کروموزوم و تولید دو کروموزوم جدید را انجام میدهد.
در اینجا متد fitness و فهمیدن طرز کارکرد آن کمی تلاش فکری بیشتری نیاز دارد. تعداد تهدیدها در متغیر collisions نگهداری میشود که در ابتدا ۰ است؛ یعنی هیچ مهرهای، دیگری را تهدید نمیکند. با توجه به این که مطمئن هستیم که دو وزیر، همزمان در یک ردیف قرار نمیگیرند (عدد صحیحی که نمایندهٔ یک ردیف است، همیشه توانی از ۲ است و در نتیجه میان بیتهای آن تنها یک بیت برابر ۱ است)، این مورد نیازی به بررسی ندارد. اما وزیر به دو صورت دیگر نیز میتواند یک مهرهٔ دیگر را تهدید کند. یکی در صورتی که مهرهای دیگر در ستونی مشترک با وزیر باشد و دیگری در صورتی که به صورت مورب، یک مهره در تیررسش باشد.
بررسی مورد اول بسیار ساده است (دو حلقهٔ for تودرتو اول در متد). در صورتی که عدد صحیح مربوط به یکی از ردیفها برابر با عدد صحیح مربوط به ردیفی دیگر باشد به این معنی است که تهدید صورت پذیرفته است و متغیر collision یک واحد به مقدارش افزوده میشود.
بررسی مورد دوم، تهدید وزیر به صورت مورب، کمی سختتر است. راهحلی که من به کار بردم شیفت دادن اعداد صحیح (مستندات مربوط به عملگرهای شیفت در پایتون) مربوط به ردیفهاست. برای مثال دو ردیف زیر را در نظر بگیرید (برای سادگی کار فرض کردم صفحه کوچکتر است):
001
010همانطور که میبینید وزیرِ ردیفِ بالاتر به صورت مورب وزیر ردیف پایینتر را تهدید میکند. حال اگر عدد صحیح مربوط به ردیف بالاتر را ۱ واحد به سمت چپ شیفت دهیم (یا برعکس، ردیف پایینی را ۱ واحد به سمت راست شیفت دهیم) میتوانیم به راحتی با مقایسهٔ این دو عدد به وجود یا عدم وجود تهدید پی ببریم. در مثال بالا ۱ واحد شیفت لازم است اما در صورتی که وزیر دیگر در ردیفهای پایینتر باشد نیازمند تعداد شیفتهای بیشتری هستیم. مثلاً در مثال زیر باید به اندازهٔ ۲ واحد شیفت دهیم:
001
000
100این که چند واحد شیفت لازم است، بهراحتی توسط اختلاف شمارهٔ ردیفها قابل محاسبه است. از آنجا که در پایتون، شیفت به راست یا چپ باید همیشه مثبت باشد، از تابع قدر مطلق (abs) استفاده شده است.
کلاس GA8
فکر میکنم تنها متدی که نیاز به کمی توضیح داشته باشد، متد run است. همینطور که مشخص است، فرایند جستوجو با الگوریتم ژنتیک نمیتواند بیشتر از تعداد مشخصی نسل ادامه پیدا کند. در صورتی که جواب مسئله زودتر پیدا شود (یک کروموزوم با fitness دقیقاً برابر ۱ که نشاندهندهٔ عدم وجود تهدید است)، حلقهٔ for شکسته میشود.
در ابتدای حلقه با استفاده از ویژگی List Comprehension پایتون مقدار fitness تمام اعضای جمعیت (تمام کروموزومها) محاسبه میشود. سپس جفتکروموزومها با هم ازدواج میکنند و فرزندانشان به offsprings اضافه میشوند. اینجا مقدار fitness یک کروموزوم هیچ تأثیری روی فرایند ازدواج ندارد و برای همچین مسئلهٔ سادهای، به نظر غیرضروری میآید. اما به صورت کلی روشهای مختلفی وجود دارد تا fitness تأثیرگذار باشد. به عنوان مثال کروموزومی که fitness بالاتری دارد شانس بیشتری برای ازدواج دارد.
بعد از حلقهٔ for درونی در متد run، فهرست جدیدی از جمعیت فعلی و فرزندانشان ایجاد میشود و بر اساس fitness مرتب میشود؛ چنان که کروموزومی که بالاترین fitness را دارد در اولین خانهٔ فهرست قرار بگیرد. با توجه به این که میخواهیم جمعیت ثابت بماند، نیمهٔ اول فهرست را برمیداریم و جای نسل فعلی را به آنها میدهیم.
پارامترها
کلاس GA8 سه پارامتر زیر را میگیرد:
mutation_rate: یک عدد اعشاری از ۰ تا ۱ که نشان میدهد در هر نسل هر کروموزوم چهقدر احتمال mutate شدن دارد.max_gen: یک عدد صحیح مثبت که حداکثر تعداد نسلهای است که برنامه اجرا میشود صرف نظر از این که به جواب برسد یا نه.pop_size: یک عدد صحیح مثبت و زوج که تعداد کروموزوم های موجود در جمعیت را نشان میدهد. در الگوریتم ژنتیک و همچین «برنامهنویسی ژنتیک» که نوعی از یادگیری ماشینی تکاملی است و از روش مشابهی با الگوریتم ژنتیک استفاده میکند، اگر جمعیت خیلی کم باشد به احتمال زیاد به جواب مناسب نمیرسیم و جمعیت را هر اندازه که بخواهیم نمیتوانیم به دلیل محدودیت منابع بزرگ انتخاب کنیم.
مباحث مرتبط
برنامهنویسی ژنتیک
برنامهنویسی ژنتیک مانند الگوریتم ژنتیک یک روش تکاملی و نوعی از یادگیری ماشینی تکاملی است. در برنامهنویسی ژنتیک کروموزومها برنامهها هستند و تلاش بر این است که بدون این که به کامپیوتر مستقیم و صریح بگوییم چه کاری میخواهیم، کامپیوتر خودش راهش را پیدا کند. یک کاربرد رایجافتادهٔ برنامهنویسی ژنتیک به عنوان مثال پیدا کردن یک تابع یا فرمول است که مجموعهای از دادهها را تخمین بزند. به این عمل اصطلاحاً symbolic regression میگویند.
یکی از کتابهایی که در این زمینه صحبت میکند، کتاب زیر از جان کوزا (John Koza) است:
- Genetic programming on the programming of computers by means of natural selection
برنامهنویسی موازی و چندرشتهای
کد پایتون بنده تنها از یک رشته (thread) و یک پروسه (process) استفاده میکند. اما این در حالی است که الگوریتم ژنتیک (و بهطبع برنامهنویسی ژنتیک) بهشدت پتانسیل موازی شدن دارد. همچنین تقریبا همهٔ رایانههای امروزی، حتی تلفنهای همراهی که روزانه استفاده میکنیم، بیشتر از ۱ هستهٔ پردازنده دارند. به عنوان یک تمرین و یادگیری میتوانید از joblib استفاده کنید تا پردازش را بین هستههای مختلف یک کامپیوتر توزیع کنید. همچین کتابخانهها و فناوریهای مختلفی وجود دارد تا بار پردازشهای بزرگ بین چندین کامپیوتر توزیع شود.




سلام
این کد خروجی ندارد
سلام ممنون از نظرتون، فاروق با اکانتش مشکل پیدا کرده برای همین یه مدت طول میکشه تا بتونه رسیدگی کنه!
سلام.
بله این کد خروجی نداره حدودا مثل یک کتابخانه نوشته شده. باید توی یه فایل ذخیره کنیدش، کلاس GA8 رو ایمپورت کنید و باهاش بازی کنید.
مثلا این یه نمونه کد هست:
from dafile import GA8
g = GA8(200, 70, 0.02)
g.run()
print(g.best())
پارامتر اول جمعیت هست که اینجا ۲۰۰ تنظیمش کردم، دوم تعداد نسلها هست که ۷۰ هست و سوم نرخ میوتیشن(فارسیش چی میشه؟) هست.
سلام
میشه لطفا یه عکس از خروجی این کد بزارین؟؟
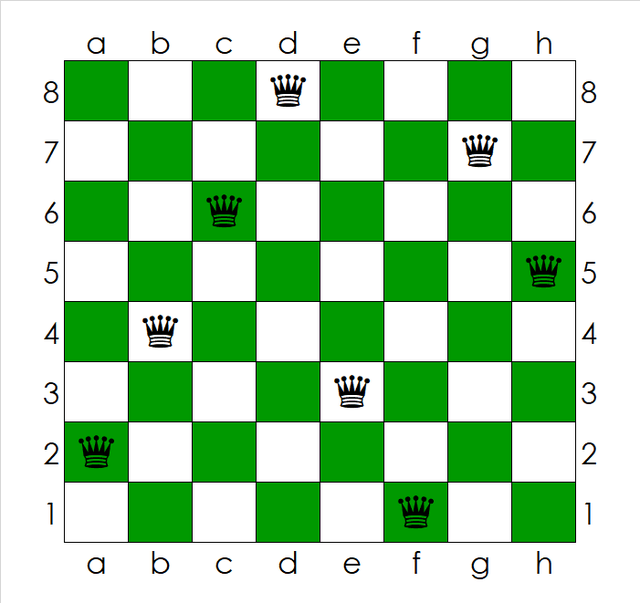
سلام. اگر دنبال یک راهحل برای مسئله هستید، تصویر اول مطلب یک راهحل نمونه هست.